Perfect Poker Coin Tosses
12 Oct 2011
We often speak of coin tosses in poker, where two players are all in with
hands that have a roughly equal chance of winning. A classic example is
AKs v QQ, here the queens
actually have a slight edge against the over-cards, with almost 54% equity.
I was wondering if there are any perfect coin tosses in Hold'em, where the players are exactly 50-50. Trivial examples exist when both players have the same hand, such as AA v AA but these consist mostly of tied outcomes, and are not particularly interesting, what of the non-trivial solutions?
Well, after running an analysis on all
possible pre-flop match-ups it turns out there aren't any, the closest
is As10s v 3s3c (or any equivalent
suit permutation) with 49.99% v 50.01% equity, close but no cigar.
Coin tosses after the flop
It's not very surprising that there are no perfect pre-flop coin tosses, as there are 48 choose 5 possible flop/turn/river combos, that's over 1.7 million outcomes that need to be perfectly divided into two groups (barring ties), highly unlikely. After the flop however there are only 45 choose 2 = 990 possible turn/river combos, much more likely that there are hands that can divide this perfectly, and in fact there are:
On the flop:
5s3h v 9h2d, Flop: 4d 2s Kh
On the turn:
Qc8s v 2d2s, Flop: 5s 5c Js, Turn: 9s
3 players on the flop:
3sAs v 4dQc v 10c8d, Flop: 6c 3c 7h
3 players on the turn:
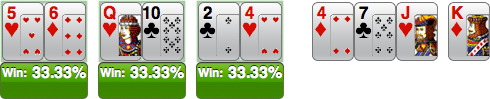5h6d v Qh10c v 2c4h, Flop: 4d 7c Jh, Turn: Kd
4 players on the turn:
2d2s v AhKs v 5s4s v 6c7h, Flop: Jd 8h Js, Turn: 9s
It's neat that none of these involve any ties in order to achieve the equal equities, it turns out that won't be possible on the flop or turn for five players, that is because there are 39 choose 2 = 741 possible turn/river combos on the flop, and 38 possible rivers on the turn, neither of these numbers are multiples of five. For six, seven and eight players these numbers do divide evenly, though I'd be quite surprised if coin tosses did exist for any of these higher number of players (then again the four player one surprised me, so who knows?).
My search algorithm that found the hands above is naive, dealing completely random hands until the criteria is met, if you have any clever ideas on how to improve the search, or if you can manually construct some other coin toss hands let me know.
Update! I was able to construct a rather contrived 5 way example on the turn where a tie occurs only ~21% of the time, and a similar 8 way example on the turn where a tie occurs 25% of the time.